
Computing

ACM Transactions on Graphics (Siggraph Asia 2024)
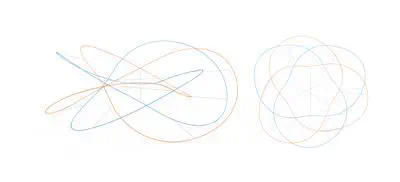
We study ensembles of elastic rods that are tensioned by a small set of inextensible cables. The cables induce forces that deform the initially straight, but flexible rods into 3D space curves at equilibrium. Rods can be open or closed, knotted, and arranged in arbitrary topologies. We specifically focus on equilibrium states with no contacts among rods. Our setup can thus be seen as a generalization of classical tensegrities that are composed of rigid rods and tensile cables, to also support rods that elastically deform. We show how this generalization leads to a rich design space, where complex target shapes can be achieved with a small set of elastic rods. To explore this space, we present an inverse design optimization algorithm that solves for the length and placement of cables such that the equilibrium state of the rod network best approximates a given set of input curves. We introduce appropriate sparsity terms to minimize the number of required cables, which significantly simplifies fabrication. Using our algorithm, we explore new classes of bending-active 3D structures, including elastic tensegrity knots that only require a few internal cables. We design and fabricate several physical models from basic materials that attain complex 3D shapes with unique structural properties.
@article{10.1145/3687967,
author = {Dandy, Liliane-Joy and Vidulis, Michele and Ren, Yingying and Pauly, Mark},
title = {Tencers: Tension-Constrained Elastic Rods},
year = {2024},
issue_date = {December 2024},
publisher = {Association for Computing Machinery},
address = {New York, NY, USA},
volume = {43},
number = {6},
issn = {0730-0301},
url = {https://doi.org/10.1145/3687967},
doi = {10.1145/3687967},
abstract = {We study ensembles of elastic rods that are tensioned by a small set of inextensible cables. The cables induce forces that deform the initially straight, but flexible rods into 3D space curves at equilibrium. Rods can be open or closed, knotted, and arranged in arbitrary topologies. We specifically focus on equilibrium states with no contacts among rods. Our setup can thus be seen as a generalization of classical tensegrities that are composed of rigid rods and tensile cables, to also support rods that elastically deform. We show how this generalization leads to a rich design space, where complex target shapes can be achieved with a small set of elastic rods. To explore this space, we present an inverse design optimization algorithm that solves for the length and placement of cables such that the equilibrium state of the rod network best approximates a given set of input curves. We introduce appropriate sparsity terms to minimize the number of required cables, which significantly simplifies fabrication. Using our algorithm, we explore new classes of bending-active 3D structures, including elastic tensegrity knots that only require a few internal cables. We design and fabricate several physical models from basic materials that attain complex 3D shapes with unique structural properties.},
journal = {ACM Trans. Graph.},
month = nov,
articleno = {214},
numpages = {13},
keywords = {computational design, physics-based simulation, elastic structures, fabrication}
}

ACM Transactions on Graphics (Siggraph 2024)
Surface-based inflatables are composed of two thin layers of nearly inextensible sheet material joined together along carefully selected fusing curves. During inflation, pressure forces separate the two sheets to maximize the enclosed volume. The fusing curves restrict this expansion, leading to a spatially varying in-plane contraction and hence metric frustration. The inflated structure settles into a 3D equilibrium that balances pressure forces with the internal elastic forces of the sheets.
We present a computational framework for analyzing and designing surface-based inflatable structures with arbitrary fusing patterns. Our approach employs numerical homogenization to characterize the behavior of parametric families of periodic inflatable patch geometries, which can then be combined to tessellate the sheet with smoothly varying patterns. We propose a novel parametrization of the underlying deformation space that allows accurate, efficient, and systematical analysis of the stretching and bending behavior of inflated patches with potentially open boundaries.
We apply our homogenization algorithm to create a database of geometrically diverse fusing patterns spanning a wide range of material properties and deformation characteristics. This database is employed in an inverse design algorithm that solves for fusing curves to best approximate a given input target surface. Local patches are selected and blended to form a global network of curves based on a geometric flattening algorithm. These fusing curves are then further optimized to minimize the distance of the deployed structure to target surface. We show that this approach offers greater flexibility to approximate given target geometries compared to previous work while significantly improving structural performance.
@article{10.1145/3658125,
author = {Ren, Yingying and Panetta, Julian and Suzuki, Seiichi and Kusupati, Uday and Isvoranu, Florin and Pauly, Mark},
title = {Computational Homogenization for Inverse Design of Surface-based Inflatables},
year = {2024},
issue_date = {July 2024},
publisher = {Association for Computing Machinery},
address = {New York, NY, USA},
volume = {43},
number = {4},
issn = {0730-0301},
url = {https://doi.org/10.1145/3658125},
doi = {10.1145/3658125},
abstract = {Surface-based inflatables are composed of two thin layers of nearly inextensible sheet material joined together along carefully selected fusing curves. During inflation, pressure forces separate the two sheets to maximize the enclosed volume. The fusing curves restrict this expansion, leading to a spatially varying in-plane contraction and hence metric frustration. The inflated structure settles into a 3D equilibrium that balances pressure forces with the internal elastic forces of the sheets.We present a computational framework for analyzing and designing surface-based inflatable structures with arbitrary fusing patterns. Our approach employs numerical homogenization to characterize the behavior of parametric families of periodic inflatable patch geometries, which can then be combined to tessellate the sheet with smoothly varying patterns. We propose a novel parametrization of the underlying deformation space that allows accurate, efficient, and systematical analysis of the stretching and bending behavior of inflated patches with potentially open boundaries.We apply our homogenization algorithm to create a database of geometrically diverse fusing patterns spanning a wide range of material properties and deformation characteristics. This database is employed in an inverse design algorithm that solves for fusing curves to best approximate a given input target surface. Local patches are selected and blended to form a global network of curves based on a geometric flattening algorithm. These fusing curves are then further optimized to minimize the distance of the deployed structure to target surface. We show that this approach offers greater flexibility to approximate given target geometries compared to previous work while significantly improving structural performance.},
journal = {ACM Trans. Graph.},
month = jul,
articleno = {87},
numpages = {18},
keywords = {deployable structure, physics-based simulation, homogenization, metamaterial, numerical optimization, computational design, fabrication}
}

ACM Siggraph 2024 Conference Papers
We introduce an algorithm to reconstruct a mesh from discrete samples of a shape’s Signed Distance Function (SDF). A simple geometric reinterpretation of the SDF lets us formulate the problem through a point cloud, from which a surface can be extracted with existing techniques. We extract all possible information from the SDF data, outperforming commonly used algorithms and imposing no topological or geometric restrictions.
@inproceedings{10.1145/3641519.3657419,
author = {Sell\'{a}n, Silvia and Ren, Yingying and Batty, Christopher and Stein, Oded},
title = {Reach for the Arcs: Reconstructing Surfaces from SDFs via Tangent Points},
year = {2024},
isbn = {9798400705250},
publisher = {Association for Computing Machinery},
address = {New York, NY, USA},
url = {https://doi.org/10.1145/3641519.3657419},
doi = {10.1145/3641519.3657419},
abstract = {We introduce an algorithm to reconstruct a mesh from discrete samples of a shape’s Signed Distance Function (SDF). A simple geometric reinterpretation of the SDF lets us formulate the problem through a point cloud, from which a surface can be extracted with existing techniques. We extract all possible information from the SDF data, outperforming commonly used algorithms and imposing no topological or geometric restrictions.},
booktitle = {ACM SIGGRAPH 2024 Conference Papers},
articleno = {23},
numpages = {12},
keywords = {point cloud, reconstruction, signed distance function},
location = {Denver, CO, USA},
series = {SIGGRAPH '24}
}
ACM Transactions on Graphics (Siggraph Asia 2023)
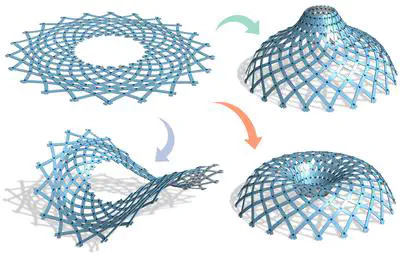
We introduce a computational pipeline for simulating and designing C-shells, a new class of planar-to-spatial deployable linkage structures. A C-shell is composed of curved flexible beams connected at rotational joints that can be assembled in a stress-free planar configuration. When actuated, the elastic beams deform and the assembly deploys towards the target 3D shape.
We propose two alternative computational design approaches for C-shells: (i) Forward exploration simulates the deployed shape from a planar beam layout provided by the user. Once a satisfactory overall shape is found, a subsequent design optimization adapts the beam geometry to reduce the elastic energy of the linkage while preserving the target shape. (ii) Inverse design is facilitated by a new geometric flattening method that takes a design surface as input and computes an initial layout of piecewise straight linkage beams. Our design optimization algorithm then calculates the smooth curved beams to best reproduce the target shape at minimal elastic energy.
We find that C-shells offer a rich space for design and show several studies that highlight new shape topologies that cannot be achieved with existing deployable linkage structures.
@article{beckerCShell,
abstract = {We introduce a computational pipeline for simulating and designing C-shells, a new class of planar-to-spatial deployable linkage structures. A C-shell is composed of curved flexible beams connected at rotational joints that can be assembled in a stress-free planar configuration. When actuated, the elastic beams deform and the assembly deploys towards the target 3D shape. We propose two alternative computational design approaches for C-shells: (i) Forward exploration simulates the deployed shape from a planar beam layout provided by the user. Once a satisfactory overall shape is found, a subsequent design optimization adapts the beam geometry to reduce the elastic energy of the linkage while preserving the target shape. (ii) Inverse design is facilitated by a new geometric flattening method that takes a design surface as input and computes an initial layout of piecewise straight linkage beams. Our design optimization algorithm then calculates the smooth curved beams to best reproduce the target shape at minimal elastic energy. We find that C-shells offer a rich space for design and show several studies that highlight new shape topologies that cannot be achieved with existing deployable linkage structures.},
author = {Becker, Quentin and Suzuki, Seiichi and Ren, Yingying and Pellis, Davide and Panetta, Julian and Pauly, Mark},
file = {/Users/yren/Zotero/storage/AC39XCIJ/weaving.pdf},
journal = {ACM Trans. Graph},
keywords = {computational design,fabrication,numerical optimization,physics-based simulation,weaving},
number = {4},
pages = {1--15},
title = {3D Weaving with Curved Ribbons},
url = {https://doi.org/10.1145/3450626.3459788},
volume = {40},
year = {2021}
}

Advances in Architectural Geometry
Deployable gridshells are a class of planar-to-spatial structures that achievea 3D curved geometry by inducing bending on a flat grid of elastic beams. However, theslender nature of these beams often conflicts with the structure’s load-bearing capacity.To address this issue, multiple layers are typically stacked to enhance out-of-planestiffness and prevent stability issues. The primary challenge then lies in deploying suchmulti-layered systems globally, as it requires significant shaping forces for actuation.This paper presents an alternative design approach that involves strategically connect-ing compact-to-volumetric gridshell components using weaving principles to shape athick segmented shell. This innovative approach allows for an incremental construc-tion process based entirely on deployable modules with volumetric configurations thatlocally provide the necessary structural depth for the entire system. To demonstrate thisprinciple, we present the realization of BamX, a research pavilion constructed usingdeployable cylindrical components made from raw bamboo slats. These componentsare interconnected at carefully optimized interlocking woven nodes, resulting in abending-active structural frame that is both strong and exceptionally lightweight. Todetermine the optimal topology and geometry of the pavilion, we employ an integrativecomputational approach that leverages advanced numerical optimization techniques.Our method incorporates a physics-based simulation of the bending and twisting be-havior of the bamboo ribbons. By finding the ideal locations for ribbon crossings, weensure that all external and internal forces are in global equilibrium while minimizingthe mechanical stress experienced by each ribbon. BamX exemplifies how a symbiosisof refined weaving craft and advanced computational modeling enables fascinatingnew opportunities for rethinking deployability in architecture.
@inbook{SuzukiMartinRenChenParaschoPauly+2023+207+220,
url = {https://doi.org/10.1515/9783111162683-016},
title = {BamX: Rethinking Deployability in Architecture through Weaving},
booktitle = {Advances in Architectural Geometry 2023},
author = {Seiichi Suzuki and Alison Martin and Yingying Ren and Tzu-Ying Chen and Stefana Parascho and Mark Pauly},
editor = {Kathrin Dörfler and Jan Knippers and Achim Menges and Stefana Parascho and Helmut Pottmann and Thomas Wortmann},
publisher = {De Gruyter},
address = {Berlin, Boston},
pages = {207--220},
doi = {doi:10.1515/9783111162683-016},
isbn = {9783111162683},
year = {2023},
lastchecked = {2023-11-23}
}
ACM Transactions on Graphics (Siggraph 2023)
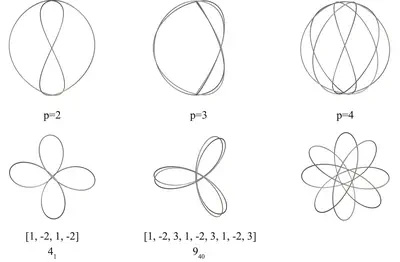
We present an algorithmic approach to discover, study, and design multistable elastic knots. Elastic knots are physical realizations of closed curves embedded in 3-space. When endowed with the material thickness and bending resistance of a physical wire, these knots settle into equilibrium states that balance the forces induced by elastic deformation and self-contacts of the wire. In general, elastic knots can have many distinct equilibrium states, i.e. they are multistable mechanical systems. We propose a computational pipeline that combines randomized spatial sampling and physics simulation to efficiently find stable equilibrium states of elastic knots. Leveraging results from knot theory, we run our pipeline on thousands of different topological knot types to create an extensive data set of multistable knots. By applying a series of filters to this data, we discover new transformable knots with interesting geometric and physical properties. A further analysis across knot types reveals geometric and topological patterns, yielding constructive principles that generalize beyond the currently tabulated knot types. We show how multistable elastic knots can be used to design novel deployable structures and engaging recreational puzzles. Several physical prototypes at different scales highlight these applications and validate our simulation.
@article{10.1145/3592399,
author = {Vidulis, Michele and Ren, Yingying and Panetta, Julian and Grinspun, Eitan and Pauly, Mark},
title = {Computational Exploration of Multistable Elastic Knots},
year = {2023},
issue_date = {August 2023},
publisher = {Association for Computing Machinery},
address = {New York, NY, USA},
volume = {42},
number = {4},
issn = {0730-0301},
url = {https://doi.org/10.1145/3592399},
doi = {10.1145/3592399},
abstract = {We present an algorithmic approach to discover, study, and design multistable elastic knots. Elastic knots are physical realizations of closed curves embedded in 3-space. When endowed with the material thickness and bending resistance of a physical wire, these knots settle into equilibrium states that balance the forces induced by elastic deformation and self-contacts of the wire. In general, elastic knots can have many distinct equilibrium states, i.e. they are multistable mechanical systems. We propose a computational pipeline that combines randomized spatial sampling and physics simulation to efficiently find stable equilibrium states of elastic knots. Leveraging results from knot theory, we run our pipeline on thousands of different topological knot types to create an extensive data set of multistable knots. By applying a series of filters to this data, we discover new transformable knots with interesting geometric and physical properties. A further analysis across knot types reveals geometric and topological patterns, yielding constructive principles that generalize beyond the currently tabulated knot types. We show how multistable elastic knots can be used to design novel deployable structures and engaging recreational puzzles. Several physical prototypes at different scales highlight these applications and validate our simulation.},
journal = {ACM Trans. Graph.},
month = jul,
articleno = {73},
numpages = {16},
keywords = {elastic knots, multistability, physics-based simulation, numerical optimization, fabrication}
}
Elastic surfaces that morph between multiple geometrical configurations are of significant engineering value, with applications ranging from the deployment of space-based photovoltaic arrays, the erection of temporary shelters, and the realization of flexible display systems, to understanding the encapsulation and release of viral RNAs. In general, ensuring that a shape with a planar rest configuration can deploy into a target three-dimensional (3D) shape is a nontrivial problem. Moreover, it is difficult to physically realize the local deformations necessary to achieve such global transformation. Here, we give a tutorial on applying conformal mapping to rationalize the geometrical deformation of several microstructure designs. A conformal map is a function that locally preserves angles and shapes but not lengths: some regions are scaled (enlarged or shrunk) more than others. To transform a planar surface to 3D, we implement uniform local scalings as mechanical deformations. Numerous natural and architected material systems exhibit such behavior, including kirigami, origami, hydrogel, linkage mechanisms, and fabric membranes. The design and fabrication of conformally transformable surfaces is a transdisciplinary challenge involving insights from advanced manufacturing, computational design, material science, and mechanics. By recognizing that many material systems exhibit isotropic deformation, we hope to inspire researchers to adopt conformal mapping in designing next-generation surface-based engineering systems.
@article{10.1115/1.4056350,
author = {Wang, Yue and Ren, Yingying and Chen, Tian},
title = {From Kirigami to Hydrogels: A Tutorial on Designing Conformally Transformable Surfaces},
journal = {Journal of Applied Mechanics},
volume = {90},
number = {4},
pages = {044801},
year = {2022},
month = {12},
abstract = {Elastic surfaces that morph between multiple geometrical configurations are of significant engineering value, with applications ranging from the deployment of space-based photovoltaic arrays, the erection of temporary shelters, and the realization of flexible display systems, to understanding the encapsulation and release of viral RNAs. In general, ensuring that a shape with a planar rest configuration can deploy into a target three-dimensional (3D) shape is a nontrivial problem. Moreover, it is difficult to physically realize the local deformations necessary to achieve such global transformation. Here, we give a tutorial on applying conformal mapping to rationalize the geometrical deformation of several microstructure designs. A conformal map is a function that locally preserves angles and shapes but not lengths: some regions are scaled (enlarged or shrunk) more than others. To transform a planar surface to 3D, we implement uniform local scalings as mechanical deformations. Numerous natural and architected material systems exhibit such behavior, including kirigami, origami, hydrogel, linkage mechanisms, and fabric membranes. The design and fabrication of conformally transformable surfaces is a transdisciplinary challenge involving insights from advanced manufacturing, computational design, material science, and mechanics. By recognizing that many material systems exhibit isotropic deformation, we hope to inspire researchers to adopt conformal mapping in designing next-generation surface-based engineering systems.},
issn = {0021-8936},
doi = {10.1115/1.4056350},
url = {https://doi.org/10.1115/1.4056350},
eprint = {https://asmedigitalcollection.asme.org/appliedmechanics/article-pdf/90/4/044801/6967926/jam\_90\_4\_044801.pdf},
}
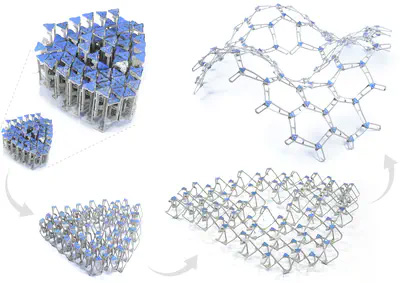
ACM Transactions on Graphics (Siggraph 2022)
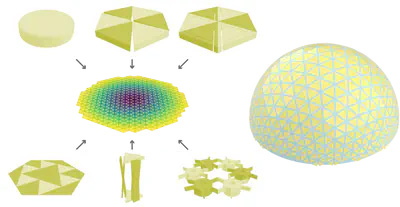
We present a computational inverse design framework for a new class of volumetric deployable structures that have compact rest states and deploy into bending-active 3D target surfaces. Umbrella meshes consist of elastic beams, rigid plates, and hinge joints that can be directly printed or assembled in a zero-energy fabrication state. During deployment, as the elastic beams of varying heights rotate from vertical to horizontal configurations, the entire structure transforms from a compact block into a target curved surface. Umbrella Meshes encode both intrinsic and extrinsic curvature of the target surface and in principle are free from the area expansion ratio bounds of past auxetic material systems.
We build a reduced physics-based simulation framework to accurately and efficiently model the complex interaction between the elastically deforming components. To determine the mesh topology and optimal shape parameters for approximating a given target surface, we propose an inverse design optimization algorithm initialized with conformal flattening. Our algorithm minimizes the structure’s strain energy in its deployed state and optimizes actuation forces so that the final deployed structure is in stable equilibrium close to the desired surface with few or no external constraints. We validate our approach by fabricating a series of physical models at various scales using different manufacturing techniques.
@article{10.1145/3528223.3530089,
author = {Ren, Yingying and Kusupati, Uday and Panetta, Julian and Isvoranu, Florin and Pellis, Davide and Chen, Tian and Pauly, Mark},
title = {Umbrella meshes: elastic mechanisms for freeform shape deployment},
year = {2022},
issue_date = {July 2022},
publisher = {Association for Computing Machinery},
address = {New York, NY, USA},
volume = {41},
number = {4},
issn = {0730-0301},
url = {https://doi.org/10.1145/3528223.3530089},
doi = {10.1145/3528223.3530089},
abstract = {We present a computational inverse design framework for a new class of volumetric deployable structures that have compact rest states and deploy into bending-active 3D target surfaces. Umbrella meshes consist of elastic beams, rigid plates, and hinge joints that can be directly printed or assembled in a zero-energy fabrication state. During deployment, as the elastic beams of varying heights rotate from vertical to horizontal configurations, the entire structure transforms from a compact block into a target curved surface. Umbrella Meshes encode both intrinsic and extrinsic curvature of the target surface and in principle are free from the area expansion ratio bounds of past auxetic material systems.We build a reduced physics-based simulation framework to accurately and efficiently model the complex interaction between the elastically deforming components. To determine the mesh topology and optimal shape parameters for approximating a given target surface, we propose an inverse design optimization algorithm initialized with conformal flattening. Our algorithm minimizes the structure's strain energy in its deployed state and optimizes actuation forces so that the final deployed structure is in stable equilibrium close to the desired surface with few or no external constraints. We validate our approach by fabricating a series of physical models at various scales using different manufacturing techniques.},
journal = {ACM Trans. Graph.},
month = jul,
articleno = {152},
numpages = {15},
keywords = {computational design, deployable structure, fabrication, numerical optimization, physics-based simulation}
}

ACM Transactions on Graphics (Siggraph 2021)
Basket weaving is a traditional craft for creating curved surfaces as an interwoven array of thin, flexible, and initially straight ribbons. The three-dimensional shape of a woven structure emerges through a complex interplay of the elastic bending behavior of the ribbons and the contact forces at their crossings. Curvature can be injected by carefully placing topological singularities in the otherwise regular weaving pattern. However, shape control through topology is highly non-trivial and inherently discrete, which severely limits the range of attainable woven geometries. Here, we demonstrate how to construct arbitrary smooth free-form surface geometries by weaving carefully optimized curved ribbons. We present an optimization-based approach to solving the inverse design problem for such woven structures. Our algorithm computes the ribbons’ planar geometry such that their interwoven assembly closely approximates a given target design surface in equilibrium. We systematically validate our approach through a series of physical prototypes to show a broad range of new woven geometries that is not achievable by existing methods. We anticipate our computational approach to significantly enhance the capabilities for the design of new woven structures. Facilitated by modern digital fabrication technology, we see potential applications in material science, bio- and mechanical engineering, art, design, and architecture.
@article{10.1145/3450626.3459788,
author = {Ren, Yingying and Panetta, Julian and Chen, Tian and Isvoranu, Florin and Poincloux, Samuel and Brandt, Christopher and Martin, Alison and Pauly, Mark},
title = {3D weaving with curved ribbons},
year = {2021},
issue_date = {August 2021},
publisher = {Association for Computing Machinery},
address = {New York, NY, USA},
volume = {40},
number = {4},
issn = {0730-0301},
url = {https://doi.org/10.1145/3450626.3459788},
doi = {10.1145/3450626.3459788},
abstract = {Basket weaving is a traditional craft for creating curved surfaces as an interwoven array of thin, flexible, and initially straight ribbons. The three-dimensional shape of a woven structure emerges through a complex interplay of the elastic bending behavior of the ribbons and the contact forces at their crossings. Curvature can be injected by carefully placing topological singularities in the otherwise regular weaving pattern. However, shape control through topology is highly non-trivial and inherently discrete, which severely limits the range of attainable woven geometries. Here, we demonstrate how to construct arbitrary smooth free-form surface geometries by weaving carefully optimized curved ribbons. We present an optimization-based approach to solving the inverse design problem for such woven structures. Our algorithm computes the ribbons' planar geometry such that their interwoven assembly closely approximates a given target design surface in equilibrium. We systematically validate our approach through a series of physical prototypes to show a broad range of new woven geometries that is not achievable by existing methods. We anticipate our computational approach to significantly enhance the capabilities for the design of new woven structures. Facilitated by modern digital fabrication technology, we see potential applications in material science, bio- and mechanical engineering, art, design, and architecture.},
journal = {ACM Trans. Graph.},
month = jul,
articleno = {127},
numpages = {15},
keywords = {weaving, physics-based simulation, numerical optimization, fabrication, computational design}
}
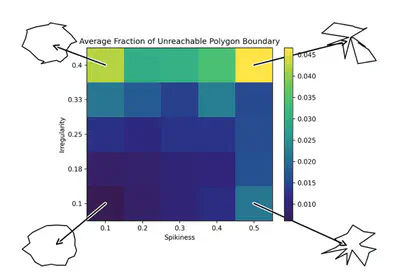
The International Journal of Robotics Research
Inspired by motion patterns of some commercially available mobile robots, we investigate the power of robots that move forward in straight lines until colliding with an environment boundary, at which point they can rotate in place and move forward again; we visualize this as the robot “bouncing” off boundaries. We define bounce rules governing how the robot should reorient after reaching a boundary, such as reorienting relative to its heading prior to collision, or relative to the normal of the boundary. We then generate plans as sequences of rules, using the bounce visibility graph generated from a polygonal environment definition, while assuming we have unavoidable non-determinism in our actuation. Our planner can be queried to determine the feasibility of tasks such as reaching goal sets and patrolling (repeatedly visiting a sequence of goals). If the task is found feasible, the planner provides a sequence of non-deterministic interaction rules, which also provide information on how precisely the robot must execute the plan to succeed. We also show how to compute stable cyclic trajectories and use these to limit uncertainty in the robot’s position.
@article{doi:10.1177/0278364921992788,
author = {Alexandra Q Nilles and Yingying Ren and Israel Becerra and Steven M LaValle},
title = {A visibility-based approach to computing non-deterministic bouncing strategies},
journal = {The International Journal of Robotics Research},
volume = {40},
number = {10-11},
pages = {1196-1211},
year = {2021},
doi = {10.1177/0278364921992788},
URL = {https://doi.org/10.1177/0278364921992788},
abstract = { Inspired by motion patterns of some commercially available mobile robots, we investigate the power of robots that move forward in straight lines until colliding with an environment boundary, at which point they can rotate in place and move forward again; we visualize this as the robot “bouncing” off boundaries. We define bounce rules governing how the robot should reorient after reaching a boundary, such as reorienting relative to its heading prior to collision, or relative to the normal of the boundary. We then generate plans as sequences of rules, using the bounce visibility graph generated from a polygonal environment definition, while assuming we have unavoidable non-determinism in our actuation. Our planner can be queried to determine the feasibility of tasks such as reaching goal sets and patrolling (repeatedly visiting a sequence of goals). If the task is found feasible, the planner provides a sequence of non-deterministic interaction rules, which also provide information on how precisely the robot must execute the plan to succeed. We also show how to compute stable cyclic trajectories and use these to limit uncertainty in the robot’s position. }
}
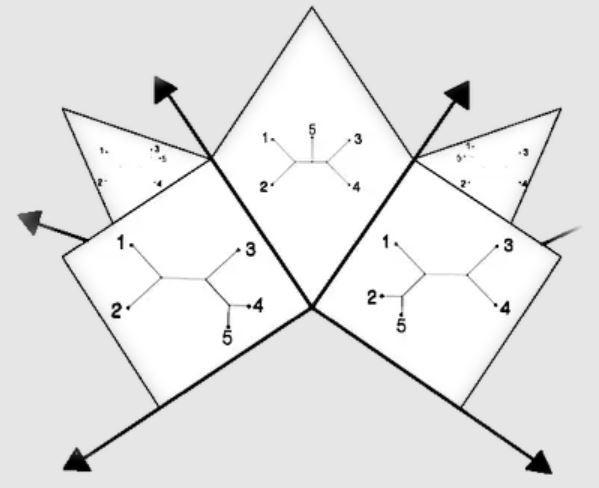
The phylogenetic tree space introduced by Billera, Holmes, and Vogtmann (BHV tree space) is a CAT(0) continuous space that represents trees with edge weights with an intrinsic geodesic distance measure. The geodesic distance measure unique to BHV tree space is well known to be computable in polynomial time, which makes it a potentially powerful tool for optimization problems in phylogenetics and phylogenomics. Specifically, there is significant interest in comparing and combining phylogenetic trees. For example, BHV tree space has been shown to be potentially useful in tree summary and consensus methods, which require combining trees with different number of leaves. Yet an open problem is to transition between BHV tree spaces of different maximal dimension, where each maximal dimension corresponds to the complete set of edge-weighted trees with a fixed number of leaves. We show a combinatorial method to transition between copies of BHV tree spaces in which trees with different numbers of taxa can be studied, derived from its topological structure and geometric properties. This method removes obstacles for embedding problems such as supertree and consensus methods in the BHV treespace framework.
@misc{ren2017combinatorialmethodconnectingbhv,
title={A combinatorial method for connecting BHV spaces representing different numbers of taxa},
author={Yingying Ren and Sihan Zha and Jingwen Bi and José A. Sanchez and Cara Monical and Michelle Delcourt and Rosemary K. Guzman and Ruth Davidson},
year={2017},
eprint={1708.02626},
archivePrefix={arXiv},
primaryClass={q-bio.QM},
url={https://arxiv.org/abs/1708.02626},
}